Schnelle Fouriertransformation (FFT)
Schnelle Fouriertransformation (FFT)
1.1 Das Realtime-Konzept der Goldammer-Messkarten
Die intelligenten Messkarten der MC4-PCI-Reihe aus dem Hause Goldammer entlasten den PC bei der Erfassung und Ausgabe von Signalen. Dies schließt eine Echtzeitverarbeitung von erfassten Signalen ein. Diese Echtzeitverarbeitung ist in unseren Treibern integriert und verlangt keine zusätzlichen Kapazitäten auf PC. Jeder Kanal kann dabei individuell konfiguriert werden.
Der Vorteil einer FFT auf dem Signalprozessor liegt in der Architektur der Prozessoren sowie in dem reduzierten Datenvolumen. Signalprozessoren können mit optimierten Algorithmen die FFT sehr schnell berechnen. Bei den Goldammer Messkarten erfolgt diese Berechnung in der Idle-Zeit des Prozessors, also wenn der Prozessor keine weiteren Aufgaben zu diesem Zeitpunkt zu erfüllen hat. Das Hostsystem wird deutlich entlastet, da es nur noch die fertigen Messwerte abholen und anzeigen muss. Die Berechnung sind so auf dem Signalprozessor verteilt, dass immer das letzte aktuelle Spektrum der FFT zur Verfügung steht. Weiterhin können natürlich auch die Zeitsignale abgerufen werden.
Erfasste Signale können auf der Karte einer schnellen Fourier-Transformation (im weiteren FFT genannt) unterzogen werden. Signale können damit in ihre Frequenzanteile zerlegt werden.
Der französische Mathematiker Fourier entdeckte, das jedes periodische Signal in viele einzelne sinus- und cosinusförmige Schwingungen zerlegt und auch durch diese nachgebildet werden kann.
Er entwickelte das mathematische Werkzeug der Fourier-Analyse. Mit einer Reihenentwicklung gelang es ihm, jedes periodische Signal durch eine unendliche Summe von mit Koeffizienten bewerteten Sinus- und Cosinus-Schwingungen zu beschreiben. Die Unendlichkeit ist eine mathematische Besonderheit, die in der Realität schwierig zu handhaben ist. Fourier wies nach, das eine endliche Anzahl von Summanden ausreichend ist, um ein periodisches Signal annähernd zu beschreiben. Durch den Abbruch der Reihenentwicklung entspricht die nachgebildete Funktion nicht mehr der Originalfunktion. Durch Verwendung von genügend Summanden kann die Originalfunktion aber beliebig genau angenähert werden.
1.2 Das Abtasttheorem oder Regeln für die Abtastung von Zeitsignalen
Für die Abtastung und die Bearbeitung von abgetasteten Signalen mit digitalen Systemen gelten einige Voraussetzungen. Diese sind:
- Das Signal muss bandbegrenzt sein, d.h. oberhalb einer Grenzfrequenz müssen alle Frequenzanteile Null sein. Die Grenzfrequenz wird „Nyquist-Frequenz“ genannt.
- Die Abtastfrequenz muss mindestens doppelt so hoch sein wie die Grenzfrequenz des Signals
Diese Regeln werden „SHANNON’sches Abtasttheorem“ genannt. Wird es nicht eingehalten, d.h. die Abtastrate ist nicht mindestens doppelt so groß wie die größte im Signalenthaltene Frequenz, treten Frequenzanteile im Spektrum auf, die im Signal eigentlich nicht enthalten sind. Dieser Effekt wird „Aliasing“ genannt und entsteht durch Spiegelung von Frequenzen oberhalb der Grenzfrequenz in den Bereich unterhalb der Grenzfrequenz. Dadurch wird sowohl das Frequenzspektrum als auch der zeitliche Verlauf des Signals verfälscht.
1.3 Arbeitsweise der FFT
Während digitale Filter in einer Einzelwertverarbeitung berechnet werden, arbeitet die FFT ausschließlich mit Datenblöcken. In diesen Datenblöcken sind die aktuellsten Abtastwerte enthalten.
Die Karten der MC4-PCI-Serie können Abtastwerte einer FFT unterziehen. Die Berechnung wird mit einen Basis-2-Algorithmus (Cooley-Tuckey) durchgeführt. Daher ist die Anzahl der Abtastwerte auf eine Potenz von 2 begrenzt (z.B. 512, 1024, 2048,…) .
Das Ergebnis ist das Frequenzspektrum des untersuchten Signals. Der FFT-Algorithmus liefert ein komplexes Spektrum. Der Realteil entspricht den Cosinus-Anteilen (), der Imaginärteil den Sinus-Anteilen ().
Durch Betragsbildung wird das Betragsspektrum gebildet.
![]()
Weitere Darstellungsarten sind:
- RMS-Spektrum
Das RMS-Spektrum ist der Effektivwert des Betragsspektrums. - Power-Spektrum
Das Power-Spektrum gibt das Quadrat der Effektivwerte an.
1.4 Beispiel: Rechteck-Signal
Im weiteren wird ein Rechteck-Signal mit einer Signalfrequenz von 100Hz betrachtet. Auf dieses Signal werden verschiedene FIR-Filter angewendet und die resultierenden Frequenzspektren mittels FFT berechnet.
Abbildung 1 zeigt den Zeitverlauf, Abbildung 2 die Frequenzspektren.
Oben ist jeweils das unbearbeitete Signal dargestellt. Neben der Frequenz bei 100Hz (der Grundfrequenz) sind im Rechteck-Signal noch weitere Frequenzen enthalten (Oberwellen). Theoretisch sind unendlich viele Oberwellen im Signal enthalten.
Der mittlere Kurvenverlauf zeigt das Rechteck-Signal nach einer FIR-Filterung mit einer Grenzfrequenz von 550Hz. Frequenzen oberhalb dieser Frequenz werden unterdrückt. Der zeitliche Verlauf weist eine starke Welligkeit auf. Im Frequenzspektrum sind nur noch 3 Frequenzanteile enthalten.
Unten wurde das Rechtecksignal einer Filterung mit der Grenzfrequenz 225Hz unterzogen. Das Filter unterdrückt alle Oberwellen, nur die Grundfrequenz bleibt erhalten. Daher wird aus dem Rechteck ein Sinussignal erzeugt.
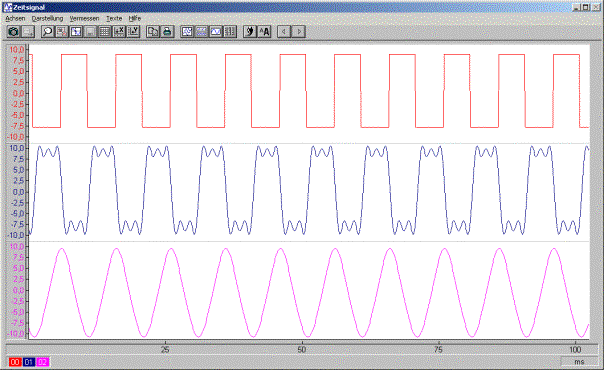
Abbildung 1: Zeitverlauf des Rechteck-Signals, oben ohne Filterung, mitte Grenzfrequenz 550Hz, unten Grenzfrequenz 225Hz
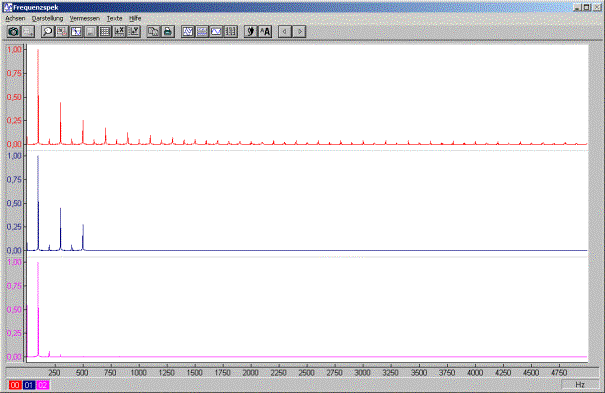
Abbildung 2: Frequenzspektren des Rechteck-Signals, oben ohne Filterung, mitte Grenzfrequenz 550Hz, unten Grenzfrequenz 225Hz

