Frequenzselektive digitale Filter
Bedeutung und Anwendung von digitalen Filtern auf abgetastete Signale
Inhaltsverzeichnis
1.1 Das Realtime-Konzept der Goldammer-Meßkarten
1.2 Das Abtasttheorem oder Regeln für die Abtastung von Zeitsignalen
1.3 Wirkungsweise digitaler Filter
1.6 Rekursive Filter (IIR-Filter)
- 1.6.1 Entwurfsverfahren
- 1.6.2 Butterworth
- 1.6.3 Chebycheff 1
- 1.6.4 Chebycheff 2
- 1.6.5 Cauer
- 1.6.6 Bessel
1.7 Nichtrekursive Filter (FIR-Filter)
- 1.7.1 Entwurfsverfahren
- 1.7.2 Fenster-Methode
- 1.7.3 Frequenzabtastung
- 1.7.4 Remez-Methode
- 1.7.5 Fensterfunktion
1.8 Vergleich IIR- und FIR-Filter
1.9 Einstellungen für digitale Filter unter DIAdem
1 Digitale Filter
1.1 Das Realtime-Konzept der Goldammer-Meßkarten
Die intelligenten Meßkarten der MC4-PCI-Reihe aus dem Hause Goldammer entlasten den PC bei der Erfassung und Ausgabe von Signalen. Dies schließt eine Echtzeitverarbeitung von erfassten Signalen ein. Diese Echtzeitverarbeitung ist in unseren Treibern integriert und somit sehr einfach zu aktivieren und konfigurieren. Jeder Kanal wird dabei individuell behandelt.
Erfasste Signale können in Echtzeit auf der Karte digital gefiltert werden. Filtern kann notwendig sein, um z.B. das Meßsignal von Störsignale zu isolieren. Dazu werden die Abtastwerte direkt nach der Wandlung einem Filteralgorithmus zugeführt. Die Bestimmung der benötigten Koeffizienten wird mit einer Programmbibliothek durchgeführt, die in unseren Treibern für die gängigsten Messerfassungssystem wie DIAdem, Dasylab und Labview eingebunden ist und erfordert somit keine zusätzlichen Programme. Der Anwender braucht nur die Bedingungen für den Filterentwurf anzugeben. Alle weiteren Arbeiten werden von unseren Treibern automatisch übernommen und ausgeführt.
1.2 Das Abtasttheorem oder Regeln für die Abtastung von Zeitsignalen
Für die Abtastung und die Bearbeitung von abgetasteten Signalen mit digitalen Systemen gelten einige Voraussetzungen. Diese sind:
- Das Signal muss bandbegrenzt sein, d.h. oberhalb einer Grenzfrequenz müssen alle Frequenzanteile Null sein.
- Die Abtastfrequenz muss mindestens doppelt so hoch sein wie die Grenzfrequenz des Signals
Diese Regeln werden „SHANNON’sches Abtasttheorem“ genannt. Wird es nicht eingehalten, d.h. die Abtastrate ist nicht mindestens doppelt so groß wie die Grenzfrequenz eines Signals, treten Frequenzanteile im Spektrum auf, die im Signal eigentlich nicht enthalten sind. Dieser Effekt wird „Aliasing“ genannt und entsteht durch Spiegelung von Frequenzen oberhalb der Grenzfrequenz in den Bereich unter der Grenzfrequenz. Die Grenzfrequenz wird „Nyquist-Frequenz“ genannt.
1.3 Wirkungsweise digitaler Filter
Abgetastete Signale sind im Allgemeinen ein Gemisch aus einem Nutzsignal (das Information enthält) und Störsignalen. Die Störsignale können Signale mit anderer Frequenz oder Rauschen sein, die dem Nutzsignal überlagert sind.
In den meisten Fällen sind die Störsignale von erheblich kleinerer Amplitude als das Nutzsignal und brauchen daher nicht berücksichtigt werden. Ist dies nicht der Fall, kann das Nutzsignal vom Störanteil verdeckt und die Informationen des Nutzsignals nicht ausgewertet werden.
Können durch eine geeignete Methode die Störanteile aus dem abgetasteten Signal entfernt werden, stehen die Informationen des Nutzsignals wieder zur Verfügung. Dabei kommen häufig selektive Filter zum Einsatz. Diese Filter machen es sich zu nutze, das die Störanteile im Allgemeinen eine andere Frequenz als das Nutzsignal haben. Sie selektieren aus dem abgetasteten Signal die Frequenzen des Nutzsignals heraus und unterdrücken alle anderen Frequenzanteile.
Die Filterung eines Signals benötigt z.T. sehr viel Rechenzeit. Um den PC von der Filterung des abgetasteten Signals zu entlasten, kann auf Karten der Firma Goldammer das abgetastete Signal gleich gefiltert und dem PC das gefilterte Signal übergeben werden.
Im letzten Teilkapitel sind Performace-Messungen abgebildet. Sie zeigen die mögliche Anzahl von Koeffizienten von FIR-Filtern in Abhängigkeit der Kanalzahl und der Summenabtastrate.
1.4 Filtertypen
Es gibt vier Standardtypen selektiver Filter:
Tiefpässe
hohe Frequenzen werden unterdrückt, tiefe Frequenzen bleiben erhalten
Hochpässe
tiefe Frequenzen werden unterdrückt, hohe Frequenzen bleiben erhalten
Bandpässe
Frequenzen innerhalb eines Bereiches bleiben erhalten, außerhalb werden sie unterdrückt
Bandsperren
Frequenzen innerhalb eines Bereiches werden unterdrückt, außerhalb bleiben sie erhalten
Es gibt darüber hinaus noch Multiband-Filter, die über mehrere Durchlass- und Sperrbereiche verfügen und weitere Filterarten, auf die hier nicht weiter eingegangen wird.
Welcher Filtertyp verwendet werden soll und wie die Durchlass- und Sperrbereiche über den Frequenzgang verteilt werden, wird über Koeffizienten festgelegt und ist damit vom Rechenalgorithmus unabhängig. Die Koeffizienten müssen allerdings für jeden Filteralgorithmus auf unterschiedliche Weise bestimmt werden und sind nicht direkt auf andere Algorithmen übertragbar. Filteralgorithmen bezeichnet man auch als Filterstrukturen
Die häufigsten Strukturen für digitale Filter sind rekursive (IIR-) und nichtrekursive (FIR-) Filter. Beide werden von Goldammer-Meßkarten unterstützt.
1.5 Das Toleranz-Schema
Das Toleranz-Schema ist die Grundlage des Filter-Entwurfs. In diesem Schema werden alle Informationen eingetragen, die der Filterentwurf benötigt.
Die notwendigen Parameter sind:
Grenzfrequenzen Sie legen die Breite des Übergangsbereiches vom Durchlass- in den Sperrbereich
fest. Je nach Filtertyp ist die Anzahl unterschiedlich.
Für jede Filterflanke wird ein Paar von Grenzfrequenzen benötigt.
Daraus folgt: Tief- und Hochpässe benötigen 2 Grenzfrequenzen, Bandpässe und Bandsperren benötigen 4 Grenzfrequenzen.
Sperrdämpfung Frequenzen im Sperrbereich sollen mindestens um diesen Wert gedämpft werden.
Durchlassdämpfung Frequenzen im Durchlassbereich dürfen höchstens um diesem Wert gedämpft
werden.
Manchmal sind zulässige Welligkeiten angegeben. Die zulässigen Welligkeiten lassen sich in Dämpfungen umrechnen und umgekehrt.
Die Breite des Übergangbereiches und die angegebene Dämpfungen legen die Filterordnung fest. Je schmaler der Übergangbereich und je höher die Sperrdämpfung desto größer wird die benötigte Filterordnung und damit der Rechenaufwand des Filters.
Das Toleranzschema kann auf mehrere Arten dargestellt werden. In den meisten Fällen werden die Dämpfungen angegeben.
Bild 1.2 zeigt ein solches Toleranzschema, bei dem die Dämpfungen angegeben werden. In
Bild 1.1 sind die zulässigen Welligkeiten eingetragen. Um das Toleranzschema zu erfüllen, darf der Frequenzgang des Filters die schraffierten Flächen nicht durchqueren. In dem Fall wäre das Toleranzschema verletzt. Um die Filterordnung zu verringern, kann von Fall zu Fall entschieden werden, ob eine geringe Verletzung des Toleranzschemas zulässig ist.
Toleranzschema eines Tiefpasses mit:
Abtastfrequenz: 1000 Hz
untere Grenzfrequenz: 100 Hz
obere Grenzfrequenz: 200 Hz
zulässige Welligkeit im Durchlassbereich: dd
zulässige Welligkeit im Sperrberech: ds

Bild 1.1: Toleranzschema mit Angabe der Frequenzen und zulässigen Welligkeiten
Statt der Welligkeiten sind im folgendem Toleranzschema die Dämpfungen angegeben. Auch hier gilt: die schraffierten Flächen dürfen vom Frequenzgang des Filters nicht durchlaufen werden.

Bild 1.2: Toleranzschema mit Angabe der Frequenzen und Dämpfungen
1.6 Rekursive Filter (IIR-Filter)
Rekursive Filtern sind Filter, bei denen das Ausgangsignal des Filters auf den Filtereingang zurückgekoppelt wird. Der Name kommt aus dem Englischen und bedeutet „infinite impuls response“ (unendliche Impulsantwort). Durch die Rückkopplung kann die benötigte Filterordnung verringert werden. Nachteilig wirkt sich allerdings die im Allgemeinen nichtlineare Phase aus.
Der Entwurf von IIR-Filtern läßt sich auf den Entwurf analoger Filter zurückführen. Dadurch kann u.a. die Ordnung bestimmt werden, die benötigt wird, um das Toleranzschema zu erfüllen. Ebenso kann der Entwurf eines Hochpass durch eine Transformation auf den Entwurf eines Tiefpasses zurückgeführt werden. Es braucht also nur ein Tiefpass bestimmt werden. Andere Filtertypen (Tiefpass, Hochpass, Bandpass, Bandsperre) lassen sich durch sogenannte Frequenztransformationen aus diesen Tiefpassprototyp berechnen. Eine Begrenzung der Koeffizienten ist nicht erforderlich. Dies ist ein großer Vorteil gegenüber den FIR-Filtern.
1.6.1 Butterworth
Geradliniger Frequenzgang im Durchlass- und Sperrbereich, dadurch keine volle Ausnutzung des Toleranzschema. Der Filtergrad ist deswegen relativ hoch. Die Gruppenlaufzeiten verändern sich kaum über den Frequenzgang.
1.6.2 Chebycheff 1
Geradliniger Frequenzgang nur im Sperrbereich und Welligkeit im Durchlassbereich, dadurch nur eine volle Ausnutzung des Toleranzschema im Durchlassbereich. Durch bessere Ausnutzung des Toleranzschemas ist der Filtergrad kleiner wie bei Butterworthfiltern. Die Gruppenlaufzeiten verändern sich leicht über den Frequenzgang.
1.6.3 Chebycheff 2
Geradliniger Frequenzgang nur im Durchlassbereich und Welligkeit im Sperrbereich, dadurch nur eine volle Ausnutzung des Toleranzschema Sperrbereich. Sonst wie bei Chebycheff 1.
1.6.4 Cauer
Welligkeit im Durchlass- sowie auch im Sperrbereich, dadurch volle Ausnutzung des Toleranzschemas. Der Filtergrad ist kleiner wie bei Chebycheff 1/2 Filtern. Die Gruppenlaufzeiten verändern sich über den Frequenzgang stark.
1.6.5 Bessel
Sehr schlechte Ausnutzung des Toleranzschemas, dadurch höherer Filtergrad als bei allen anderen Filtertypen. Die Gruppenlaufzeiten sind über den gesamten Frequenzgang nahezu konstand.
1.7 Nichtrekursive Filter (FIR-Filter)
Nichtrekursive Filter sind Filter, bei denen das Ausgangssignal des Filters nicht auf den Filtereingang zurückgekoppelt wird. Der Name kommt aus dem Englischen und bedeutet „finite impuls response“ (endliche Impulsantwort). Diese Filtertypen sind immer stabil. Mit ihnen ist es möglich, ohne zusätzlichen Aufwand eine lineare Phase und damit eine konstante Gruppenlaufzeit zu realisieren. Dieser Vorteil gegenüber den IIR-Filtern wird durch eine höhere Filterordnung erkauft.
Der Entwurf von FIR-Filtern läßt sich nicht auf den Entwurf analoger Filter zurückführen. Ebenso kann die Ordnung nicht bestimmt werden, die benötigt wird, um das Toleranzschema zu erfüllen. Dies führt zu Try-And-Fail-Vorgehensweise, bei der das Entwurfsverfahren rekursiv durchgeführt wird. Dabei wird bei jedem Durchgang die Ordnung erhöht und geprüft, ob das Toleranzschema erfüllt wird. Bei Erfüllung wird die Rekursion abgebrochen. Es sind auch keine Transformationen bekannt, durch die man einen Tiefpass in einen anderen Filtertyp, z.B. Hochpass, umwandeln kann. Jedes Entwurfsproblem muss neu gelöst werden.
1.7.1 Entwurfsverfahren
Der Treiber für die Karten aus dem Hause Goldammer unterstützen mehrere Entwurfsverfahren zur Berechnung von Koeffizienten für FIR-Filter. Jedes Entwurfsverfahren kann Tiefpässe, Hochpässe, Bandpässe, und Bandsperren berechnen.
Da die Ordnung eines FIR-Filters nicht absolut berechnet werden kann, ist eine zusätzliche Funktion implementiert, die anhand des Toleranzschemas die Ordnung bestimmt, mit der das Toleranzschema erfüllt wird. Dieses kann allerdings einige Zeit in Anspruch nehmen, da das Entwurfsverfahren rekursiv wiederholt wird, bis die richtige Ordnung gefunden wurde.
1.7.2 Fenster-Methode
Bei der Fenster-Methode wird eine Impulsantwort berechnet. Dazu werden Funktionen benutzt, mit denen die Koeffizienten direkt berechnet werden können. Allerdings ist auf diese Weise nur eine lineare Phase realisierbar.
Die berechnete Impulsantwort wird in ihrer Länge begrenzt. Wird die Impulsantwort abgeschnitten, so spricht man von einer Begrenzung mit einem Rechteckfenster. Dieses führt zu Überschwingungen an Filterflanken. Diese Überschwinger werden mit zunehmenden Abstand zur Flanke kleiner. Eine Erhöhung der Ordnung reduziert die Überschwingeramplituden nicht. Durch Verwendung einer anderen Fensterfunktion, die die Impulsantwort nicht abschneidet, sondern die Koeffizienten an den Rändern immer stärker gegen Null dämpft. Auf diese Weise werden die Überschwinger stark reduziert. Dies wird erkauft durch eine weniger steile Flanke. In (1.7.5) sind die Funktionsverläufe einiger Fensterfunktionen abgebildet.
In den folgenden Bildern sind Frequenzgänge von Filtern mit unterschiedlicher Ordnung dargestellt. Es ist erkennbar, dass die Überschwinger durch Erhöhung der Ordnung nicht verschwinden, sondern sie sich nur in einem kleineren Bereich um die Flanke konzentrieren. Das Hanning-Fenster reduziert die Überschwinger deutlich, allerdings verläuft die Flanke weniger steil.

Bild 1.3: Frequenzgang eines Filter 20.Ordnung entworfen mit der Fenster-Methode. Deutlich zu erkennen ist die Welligkeit durch Verwendung des Rechteckfenster. Das Hanning-Fenster reduziert die Welligkeit, verrringert aber die Flankensteilheit.

Bild 1.4: Frequenzgang eines Filters 60.Ordnung entworfen nach der Fenstermethode. Die Flanke wurde steiler, die Welligkeit nimmt aber nicht ab.
1.7.3 Frequenzabtastung
Die Frequenzabtastung erzeugt aus einem Frequenz- und einem Phasengang eine Impulsantwort mit Hilfe der inversen FFT. Der Vorteil ist hier, das beliebige Frequenz- und Phasengänge realisiert werden können. Der Rechenaufwand wird hauptsächlich durch die FFT bestimmt. Die Filterordnung spielt eine untergeordnete Rolle.
Die hier berechneten Koeffizienten bilden nur eine Näherung der wirklichen Impulsantwort. Die Genauigkeit läßt sich durch Erhöhung der FFT-Punkte vergrößern. Die benötigte Rechenzeit steigt dadurch aber stark an.
Das Problem der Überschwinger an Filterflanken tritt hier auch auf. Durch Verwendung von Fensterfunktionen lassen sich diese Überschwinger auf Kosten einer weniger steilen Flanke verringern.
1.7.4 Remez-Methode
Die Remez-Methode erzeugt Filter-Koeffizienten, die als „equi-ripple-filters“ bekannt sind. Eine andere Bezeichnung ist „optimale FIR-Filter“. Die nach dieser Methode entworfenen Filter sind in der Hinsicht optimal, das sie das Toleranzschema im Durchlass- und Sperrbereich optimal ausfüllen. Dadurch entsteht sowohl im Durchlass- als auch im Sperrbereich eine gleichmäßige Welligkeit (ähnlich dem Tschebyscheff3‑IIR‑Filter). Desweiteren benötigen diese Filter häufig eine geringere Ordnung zur Erfüllung des Toleranzschemas als die oben genannten Entwurfsverfahren.
Ein Nachteil ist der hohe Rechenaufwand. Dafür bietet dieses Entwurfsverfahren eine große Flexibilität.

Bild 1.5: Frequenzgang eines Filters 20.Ordnung entworfen mit der Remez-Methode.
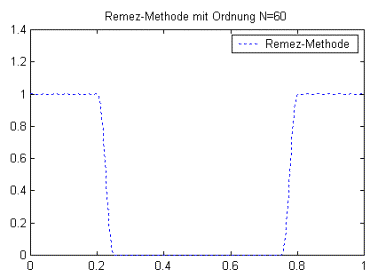
Bild 1.6: Frequenzgang eines Filters 60.Ordnung entworfen mit der Remez-Methode.
Bei der Remez-Methode ist eine Fenster-Funktion nicht notwendig. Mit steigender Ordnung wird die Welligkeit geringer.
1.7.5 Fensterfunktion
Diese Entwurfsmethode erzeugt nur eine Fensterfunktion und übergibt diese der aufrufenden Routine. Die Anzahl der Koeffizienten der Fensterfunktion ist die übergebene Ordnung plus Eins. Es sind über 200 Fensterfunktionen bekannt. Die am häufigsten verwendeten Fensterfunktionen werden von unserem Treiber angeboten.
Im Bild unten sind verschiedene Fensterfunktionen dargestellt.

Bild 1.7: Funktionverlauf einiger Fensterfunktionen
1.8 Vergleich IIR- und FIR-Filter
Ein direkter Vergleich zwischen IIR- und FIR-Filtern ist nicht möglich. Der Benutzer muss in Anhängigkeit der Aufgabe und Randbedingungen entscheiden, welcher Filterart zum Einsatz kommen soll. Dazu müssen die Vorteile und Nachteile der beiden Filterarten gegeneinander abgewägt werden. Die nachfolgende Tabelle soll dazu eine Hilfe bieten:
| FIR-Filter | IIR-Filter | ||
| Vorteile | Nachteile | Vorteile | Nachteile |
| immer stabil | nicht immer stabil, daher Stabilität nachprüfen | ||
| konstante (lineare) Gruppenlaufzeit | variable (nichtlineare) Gruppenlaufzeit | ||
| Ausgangssignal wird nicht verfälscht | Ausgangssignal wird verfälscht | ||
| endliche Impulsantwort, dadurch Überschwinger an Sprungstellen | Unendliche Impulsantwort, dadurch keine Überschwinger an Sprungstellen | ||
| höhere Ordnung nötig zur Erfüllung des Toleranzschemas als bei IIR | niedrigere Ordnung nötig zur Erfüllung des Toleranzschemas als FIR | ||
| große Gruppenlaufzeiten und hoher Rechenaufwand | kleinere Gruppenlaufzeiten und niedrigerer Rechenaufwand | ||
1.9 Einstellungen für digitale Filter unter DIAdem

Bild 1.8: Eingabemaske für Filter unter DIAdem
Um Filter zu aktivieren und zu konfigurieren, klicken Sie auf „Gerät..“. Auf dem sich öffnenden Dialog sind oben die verschiedenen Einstellungsmöglichkeiten aufgeführt.
- Auf dieser Seite werden die Eingänge konfiguriert.
- Hier befinden sich die Einstellungen für den Filter eines Kanals, der unter (3) ausgewählt werden kann. Die Einstellungen auf dieser Seite können für jeden Kanal individuell festgelegt werden.
- Hier können Sie einen Kanal auswählen, den Sie konfigurieren möchten. Ist der gewählte Kanal konfiguriert, kann hier gleich der nächste Kanal ausgewählt werden.
- An dieser Stelle können Sie für den unter (3) gewählten Kanal festlegen, ob die Abtastwerte dieses Kanals einer Filterung unterzogen werden sollen.
- Auswahl der Filterstrukturen (rekursive IIR- oder nichtrekursive FIR-Filter). Die hier gewählte Filterstruktur beeinflusst die Bedeutung und Einträge anderer Eingabefelder.
- Festlegung des Filtertyps. Mögliche Einstellungen: Tiefpass, Hochpass, Bandpass, Bandsperre
- Grenzfrequenzen der 1.Filterflanke, links die untere, rechts die obere Grenzfrequenz der Flanke. Die Angabe dieser Flanke wird für Tiefpass und Hochpass benötigt. Bei diesen Typen wird die 2.Flanke ingnoriert.
- Grenzfrequenzen der 2.Filterflanke, links die untere, rechts die obere Grenzfrequenz der Flanke. Die Angabe dieser Flanke wird zusätzlich für Bandpass und Bandsperre benötigt.
- Frequenzen können absolut (in Hz) oder normiert angegeben werden. Normierte Frequenzen haben den Vorteil, das die Abtastfrequenz nicht berücksichtigt werden braucht. Absolute Frequenzen können in normierte Frequenzen umgerechnet werden, wenn die Abtastrate bekannt und gegeben ist. Die Abtastfrequenz wird bei der Einstellung „absolute Frequenzen“ bei der Initialisierung aus dem Taktblock übernommen.
- Die Dämpfungen im Durchlass- und im Sperrbereich werden hier angegeben.
Links die Durchlassdämpfung, rechts die Sperrdämpfung. Die Sperrdämpfung sollte immer größer sein wie die Durchlassdämpfung. - Dämpfungen können auch als Angabe von zulässigen Welligkeiten angegeben werden. Eine Umrechnung wird intern vorgenommen. Hier wird angegeben, ob die Eingabe als Dämpfung oder als Welligkeit interpretiert werden soll.
- Hier wird das Entwurfsverfahren angegeben. An dieser Stelle muss unterschieden werden, welche Filterstruktur unter (5) gewählt wurde. Vorteile, Nachteile und Besonderheiten der Entwurfsverfahren sind oben erläutert.
FIR-Filter Fenstermethode, Frequenzabtastung, Remez-Methode, Fensterfunktion
IIR-Filter Butterworth, Tschebyscheff 1, Tschebyscheff 2, Cauer - Dieses Feld dient der Auswahl der Fensterfunktion, mit der die Koeffizienten bewertet werden sollen, um die Welligkeiten der Filterflanken zu minimieren.
Diese Auswahl steht nur für FIR-Filter zur Verfügung. - Ein Klick auf dieses Feld öffnet ein Fenster, in dem der Frequenzgang und die Gruppenlaufzeit des Filters dargestellt wird. So kann sich der Benutzer einen visuellen Überblick über das Verhalten des von ihm definierten Filters verschaffen.
- Sind alle für alle Kanäle die Parameter eingestellt, kann hierüber das Konfigurationsfenster geschlossen werden.
1.10 Einstellungen für digitale Filter unter Dasylab
Digitale Filter werden unter Dasylab nur mit dem Extension-Toolkit unterstützt.

Bild 1.9: Eingabemaske für Filter unter Dasylab
Dieses Dialogfeld öffnen Sie durch klicken auf das Feld „Filtereinstellungen“ im Konfigurationsdialog des gewählten Blocks.
- An dieser Stelle können Sie für den gewählten Kanal festlegen, ob die Abtastwerte dieses Kanals einer Filterung unterzogen werden sollen.
- Auswahl der Filterstrukturen (rekursive IIR- oder nichtrekursive FIR-Filter). Die hier gewählte Filterstruktur beeinflusst die Bedeutung und Einträge anderer Eingabefelder.
- Festlegung des Filtertyps. Mögliche Einstellungen: Tiefpass, Hochpass, Bandpass, Bandsperre
- Frequenzen können absolut (in Hz) oder normiert angegeben werden. Normierte Frequenzen haben den Vorteil, das die Abtastfrequenz nicht berücksichtigt werden braucht. Absolute Frequenzen können in normierte Frequenzen umgerechnet werden, wenn die Abtastrate bekannt und gegeben ist. Hier werden auch die Grenzfrequenzen der 1. und 2.Filterflanke eingetragen. Links wird jeweils die untere, rechts die obere Grenzfrequenz der Flanke festgelegt. Tiefpässe und Hochpässe benötigen nur die 1.Filterflanke, die 2.Flanke wird ignoriert.’
Bandpässe und Bandsperren benötigen zusätzlich die Angabe der 2.Filterflanke. - Dämpfungen können auch als Angabe von zulässigen Welligkeiten angegeben werden. Eine Umrechnung wird intern vorgenommen. Hier wird angegeben, ob die Eingabe als Dämpfung oder als Welligkeit interpretiert werden soll. Hier werden auch die Dämpfungen im Durchlass- und im Sperrbereich angegeben. Die Sperrdämpfung sollte immer größer sein wie die Durchlassdämpfung.
- Hier wird das Entwurfsverfahren angegeben. An dieser Stelle muss unterschieden werden, welche Filterstruktur unter (5) gewählt wurde. Vorteile, Nachteile und Besonderheiten der Entwurfsverfahren sind oben erläutert.
FIR-Filter Fenstermethode, Frequenzabtastung, Remez-Methode, Fensterfunktion
IIR-Filter Butterworth, Tschebyscheff 1, Tschebyscheff 2, Cauer - Dieses Feld dient der Auswahl der Fensterfunktion, mit der die Koeffizienten bewertet werden sollen, um die Welligkeiten der Filterflanken zu minimieren.
Diese Auswahl steht nur für FIR-Filter zur Verfügung. - Ein Klick auf dieses Feld öffnet ein Fenster, in dem der Frequenzgang und die Gruppenlaufzeit des Filters dargestellt wird. So kann sich der Benutzer einen visuellen Überblick über das Verhalten des von ihm definierten Filters verschaffen.
- Sind alle Parameter eingestellt, kann hierüber das Konfigurationsfenster geschlossen werden.
1.11 Leistungsdaten
Die Leistungsmessungen wurden mit folgendem Messystem durchgeführt:
PC:
- Prozessor: AMD K6-200
- Speicher: 128MB PC-100 (DIMM)
- Mainboard: Asus P5A B
- Chipsatz: ALI
- Grafikkarte: Diamond Viper AGP (RIVA 128)
Meß-Software:
- DIAdem 7.02
- Messung im Hardwaretakt
- Anzeige durch Graphen
- DLL-Version: 5.2.0.0
- DSP-Treiber: 5.2.1.1
Meß-Karte:
- MC4Light/HS der Firma Goldammer
1.11.1 FIR-Filter

Es lassen sich einige Schlussfolgerungen aus diesen Daten ziehen:
- Bei konstanter Summenabtastrate bleibt die Anzahl der Koeffizienten pro Kanal nahezu konstant.
- Eine Veränderung der Summenabtastrate um den Faktor a erhöht die Anzahl der Koeffizienten pro Kanal um den Faktor 1/a .
- Die Gesamtanzahl der Koeffizienten steigt mit der Anzahl der Kanäle nahezu linear.
- Die Änderung der Anzahl der Koeffizienten pro Kanal beträgt real 1/ ( a – 1,5%..5% ). Verringerung der Abtastrate erhöht die Anzahl der möglichen Koeffizienten pro Kanal um einen Faktor, der um ca. 1,5%..5% mehr Koeffizienten ermöglicht.

